七年的投入产出表#

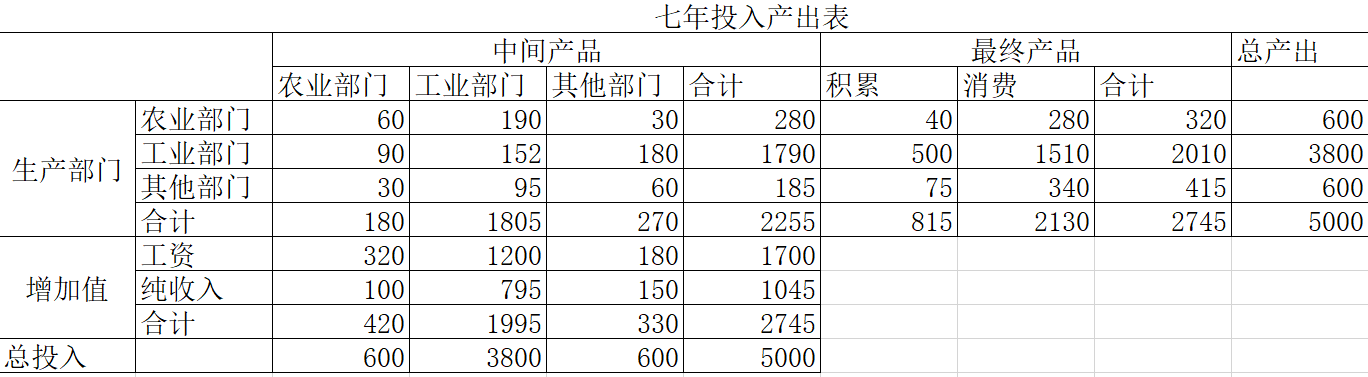
1557569224487

1.计算直接消耗系数和完全消耗系数（保留4位小数）

答：

$\notag a_{ij}=\frac {X_{ij}}{X_{j}}\\ \mathbf{A} = \left( \begin{array}{ccc} a_{11} & a_{12} & \ldots \\ a_{21} & a_{22} & \ldots \\ \vdots & \vdots & \ddots \end{array} \right) = \left( \begin{array}{ccc} 0.1 & 0.05 & 0.05\\ 0.15 & 0.4 & 0.3\\ 0.05 & 0.025 & 0.1 \end{array} \right)\\ A:直接消耗系数矩阵$ $\notag \mathbf{I} - \mathbf{A} = \left( \begin{array}{ccc} 0.9 & -0.05 & -0.05\\ -0.15 & 0.6 & -0.3\\ -0.05 & -0.025 & 0.9 \end{array} \right)\\$ $\notag \mathbf{B} = ( I - A)^{-1}-I= \left( \begin{array}{ccc} 0.1328 & 0.0984 & 0.0957\\ 0.3191 & 0.7179 & 0.5903\\ 0.0718 & 0.0531 & 0.1328 \end{array} \right)\\ B:完全消耗系数$

2.若t+1年的农业、工业和其他部门的最终产品供给量分别增长4%，11%，15%。则预测国民经济各部门的总产出和中间消耗的需求量各位多少？

答：

由题目得到t+1年得到农业，工业和其他部门得最终产品供给量分别为332.8，2231.1，477.25亿元，

即
$\notag y_{农业} = 320*（1+4\%）=332.8\\ y_{工业} = 2010*(1+11\%)=2231.1\\ y_{其他} = 415*(1+15\%) = 447.25\\ \mathbf{Y}=\left( \begin{array}\\ 332.8 & 2231.1 & 477.25 \end{array} \right)^T$
设X~i~(i = 1,2,3)表示第i部门的总产品

已知$\mathbf{A} = \left( \begin{array}{ccc}
0.1 & 0.05 & 0.05\
0.15 & 0.4 & 0.3\
0.05 & 0.025 & 0.1
\end{array} \right)$

可以求得
$\notag \mathbf{I} - \mathbf{A} = \left( \begin{array}{ccc} 0.9 & -0.05 & -0.05\\ -0.15 & 0.6 & -0.3\\ -0.05 & -0.025 & 0.9 \end{array} \right)\\$
所以
$\notag \mathbf{X} = (\mathbf{I} - \mathbf{A})^{-1}\mathbf{Y} \\ = \begin{eqnarray*} \left( \begin{array}\\ 639.3418 & 4202.9414 & 649.2118 \end{array} \right) \end{eqnarray*} ^T$
由 $\mathbf{x{ij} = a{ij}x_{j}}$ (i,j = 1,2,3)

计算得到
$\notag X_{ij} = \left( \begin{array}{ccc} 63.9342 & 210.1471 & 32.4606\\ 95.9013 & 1681.1766 & 194.7635\\ 31.9671 & 105.0735 & 64.9212 \end{array} \right)$
所以预测

国民经济各部门的总产出$\left( \begin{array}{ccc}
639.3418 & 4202.9414 & 649.2118
\end{array} \right) ^T$

中间消耗的需求量各为

$\left(
\begin{array}{ccc}
63.9342 & 210.1471 & 32.4606\
95.9013 & 1681.1766 & 194.7635\
31.9671 & 105.0735 & 64.9212
\end{array}
\right)$

3.当t+1年GDP为3187.5亿元，其中农业，工业和其他部门的增加值分别为600亿元，2137.5亿元，450亿元，则预测t+1年的国民经济总产出，最终产品与中间产品的需求量将达到多少？

答：

设Z~j~(j = 1,2,3)为第j部门新创造的价值

根据核算GDP收入法得 $\mathbf{Z} =\left( \begin{array}\ 600 & 3137.5 & 450 \end{array} \right) ^T $
$\notag \mathbf{D} = \left( \begin{array}{ccc} 0.3 & 0 & 0\\ 0 & 0.475 & 0\\ 0 & 0 & 0.45 \end{array} \right)\\$ $\notag \mathbf{X} = (I -D)^{-1}Z\\ = \left( \begin{array} 857.1429 & 5976.1905 & 818.1818 \end{array}\right)^T\\$ $\notag \mathbf{I} - \mathbf{A} = \left( \begin{array}{ccc} 0.9 & -0.05 & -0.05\\ -0.15 & 0.6 & -0.3\\ -0.05 & -0.025 & 0.9 \end{array} \right)\\$ $\notag \mathbf{Y} = (I-A)X\\ = \left( \begin{array}\\ 431.7100 & 3211.6883 & 544.1017 \end{array} \right)$
由 $\mathbf{x{ij} = a{ij}x_{j}}$ (i,j = 1,2,3)
$\notag X_{ij} = \left(\begin{array}{ccc} 85.7143 & 298.8096 & 40.9091\\ 128.5714 & 2390.4762 & 245.4545\\ 42.8571 & 149.4048 & 81.8182 \end{array}\right)$
所以预测t+1年的国民经济

总产出为

$(\begin{array}
857.1429 & 5976.1905 & 818.1818
\end{array})$

最终产品需求量将达到

$\left(
\begin{array}\
431.7100 & 3211.6883 & 544.1017
\end{array}
\right)$

中间产品的需求量将达到

$\left(\begin{array}{ccc}
85.7143 & 298.8096 & 40.9091\
128.5714 & 2390.4762 & 245.4545\
42.8571 & 149.4048 & 81.8182
\end{array}\right)$

4.若假定工业部门的最终产品供给量增加150亿元，分析各部门应配置的劳动力数量（假设农业、工业和其他部门的每年工资水平分别为5000元/人，10000元/人，10000元/人）

答：

劳动者报酬系数 = 劳动者报酬/总产出： $\overline{A_{ij}}$

$V = \overline{A_{ij}}(I+B)\Delta Y $

$\overline{A_{ij} }= ( \begin{array}\
\frac{320}{600} & 0 & 0\
0 & \frac{1200}{3800} & 0\
0 & 0 & \frac{180}{600}
\end{array})$

$I+B = \left(\begin{array}{ccc}
1.1328 & 0.0984 & 0.0957\
0.3191 & 1.7179 & 0.5903\
0.0718 & 0.0532 & 1.1328
\end{array} \right)$

$\Delta{Y} = (\begin{array}\
0 & 150 & 0 \
\end{array} )^T$
$\notag \mathbf{V} = (\begin{array}\\ 7.8713 & 81.3722 & 2.3933 \end{array})^T$
劳动者数量 = 劳动者报酬数量 / 每年工资水平

$\therefore 农业部门劳动者数量：7.871310^8/(510^3) = 157426$

$\therefore 工业部门劳动者数量：81.372210^8/(110^4) = 813722 $

$\therefore 其他部门劳动者数量：2.393310^8/(110^4) = 23933$

5.计算影响力系数和感应度系数

答：

影响力系数：
$\notag \mathbf{F}_{j} = \frac{\sum_{i=1}^n\overline{b_{ij}}}{\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{n}\overline{b_{ij}}}(j =1,2,\cdots,n)$ $\notag \mathbf{\overline{b_{ij}}} = \left(\begin{array}{ccc} 1.1328 & 0.0984 & 0.0957\\ 0.3191 & 1.7179 & 0.5903\\ 0.0718 & 0.0532 & 1.1328 \end{array}\right)$
$农业\sum{i=1}^n\overline{b{ij}} = 1.1328+0.3191+0.0718 = 1.5237$

$工业\sum{i=1}^n\overline{b{ij}} = 0.0984+1.7179+0.0532 = 1.8695$

$其他\sum{i=1}^n\overline{b{ij}} = 0.0957+0.5903 +1.1328=1.8188$

$\frac{1}{n}\sum{i=1}^{n}\sum{j=1}^{n}\overline{b_{ij}} = 1.7373$

$\therefore \农业部门的影响力系数：1.5237 / 1.7373 = 0.8771 \ 工业的影响力系数：1.8695/1.7373 = 1.0761\其他部门的影响力系数：1.8188/1.7373 = 1.0469$

感应度系数：
$\notag \mathbf{E_i}= \frac{\sum_{j=1}^n\overline{b_{ij}}}{\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{n}\overline{b_{ij}}}$
$农业\sum{j=1}^n\overline{b{ij}} = 1.1328+0.0984+0.0957 = 1.3269$

$工业\sum{j=1}^n\overline{b{ij}} = 0.3191+1.7179+0.5903=2.6273$

$其他\sum{j=1}^n\overline{b{ij}} = 0.0718+0.0532+1.1328=1.2578$

$\frac{1}{n}\sum{i=1}^{n}\sum{j=1}^{n}\overline{b_{ij}} = 1.7373$

$\therefore \农业部门的感应度系数：1.3269/ 1.7373 = 0.7638\ 工业部门的感应度系数：2.6273/1.7373 = 1.5123\其他部门的感应度系数：1.2578/1.7373 = 0.7240$